Bonjour à tous,
Vous ne le saviez peut-être pas, mais cette semaine, c'est la semaine des mathématiques ! À cette occasion, l'envie m'a pris de partager un peu de mon savoir mathématique avec vous, me permettant ainsi d'exposer du vocabulaire spécifique que l'on peut retrouver dans notre jeu. L'occasion est d'autant plus belle qu'il s'agit du 100ème article à paraître sur le blog, et je voulais célébrer ce succès à ma manière ! Et qui sait, peut-être parviendrai-je à réconcilier certains d'entre vous avec cette discipline qui regorge de richesses !
 |
| Bienvenue dans l'univers psychédélique des mathématiques ! |
Cet article n'a pas pour vocation d'être exhaustif; il se peut d'ailleurs certainement que j'oublie certains termes. Il ne s'agit pas non plus d'un cours de mathématiques. Mon ambition, beaucoup plus modeste, et de vous présenter un aperçu des principaux domaines d'étude en mathématiques, et bien sûr de vous donner un peu de vocabulaire. Je vais donc tâcher de vulgariser mon propos, quitte à omettre des détails techniques pour éviter de vous noyer dans toute la complexité de cette discipline !
Les mathématiciens
Les mathématiques ont une histoire très riche qui s'étend sur plusieurs millénaires. Qui ne connaît pas Pythagore, connu pour son célèbre théorème, originaire de la Grèce antique, au VIème siècle avant J.-C. ? Nombreux sont les mathématiciens qui au fil du temps ont contribué au développement et à l'essor des mathématiques telles que nous les connaissons aujourd'hui. On retrouve quelques-uns de ces savants dans notre glossaire sous forme d'adjectifs :
- népérien, ienne, du théologien, physicien, astronome et mathématicien écossais des XVIème et XVIIème siècles John Napier (parfois francisé en Jean Neper), particulièrement remarqué pour son invention des logarithmes, dont le fameux logarithme népérien.
 |
| John Napier |
- newtonien, de Isaac Newton, savant anglais puis britannique des XVIIème et XVIIIème siècles, qui s'est illustré en mathématiques, mais également en philosophie, physique, alchimie, astronomie et théologie. Il révolutionne la mécanique dite aujourd'hui « classique » ou « newtonienne », en énonçant les trois lois universelles du mouvement des corps. On utilise d'ailleurs le newton, unité de mesure de la force. En analyse numérique, la méthode qu'il développe pour l'approximation d'une solution d'une équation, appelée « méthode de Newton », est tout bonnement phénoménale, et trouve de multiples applications.
 |
| Isaac Newton |
Permettez-moi une digression afin de vous donner un bref aperçu de cette méthode, appliquée au calcul de la racine carrée d'un nombre. La racine carrée d'un nombre x est le nombre qui, multiplié par lui-même, donne x. Par exemple, la racine carrée de 9 est 3 car 3 x 3 = 9, de même que la racine carrée de 121 est 11 car 11 x 11 = 121. Mais qu'en est-il de la racine carrée de 2 ? Le résultat n'est pas entier et vaut environ 1,414. Essayez donc de calculer 1,414 x 1,414 : vous allez retrouver pratiquement 2. Toutefois, peut-on être plus précis ? La méthode de Newton, dont je vous passe les détails techniques, suggère de construire une suite de nombres comme ci-après. Prenons au départ n'importe quel nombre, par exemple u0 = 1. Le prochain nombre u1 se calcule en appliquant la règle suivante :
u1 = u0⁄2 + 1⁄u0 = 1⁄2 + 1⁄1 = 1,5.
En appliquant cette même règle, on calcule u2 :
u2 = u1⁄2 + 1⁄u1 = 1,5⁄2 + 1⁄1,5 = 1,41666...
Cela ne vous rappelle-t-il pas quelque chose ? En poursuivant ainsi, les nombres calculés sont de plus en précis. La force de la méthode de Newton provient du fait qu'à chaque nombre calculé, le nombre de décimales exactes double par rapport au précédent. Elle permet donc d'obtenir très rapidement une excellente approximation de la vraie valeur de la racine carrée de 2 dans le cas présent.
- leibnizien (sous-tops : bélizien, zibeline), de Gottfried Wilhelm Leibniz, philosophe, scientifique, mathématicien, logicien, diplomate, juriste, bibliothécaire et philologue allemand des XVIIème et XVIIIème siècles. On lui doit, avec Newton d'ailleurs, les fondements du calcul infinitésimal moderne, branche des mathématiques dédié aux quantités infiniment petites, comprenant le calcul différentiel et le calcul intégral.
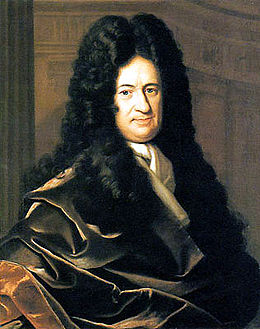 |
| Gottfried Wilhelm Leibniz |
- abélien, ienne (anagramme : baleine), du mathématicien norvégien Niels Henrik Abel du début du XIXème siècle, mort à l'âge de 26 ans uniquement de la tuberculose. Ses travaux sont multiples, aussi bien en analyse numérique qu'en algèbre sur les résolutions des équations. On parle par exemple de groupe abélien... vous en connaissez tous au moins un ! Je parle de l'ensemble des nombres réels muni de l'addition; dire qu'il est abélien signifie que pour tous nombres a et b, a + b = b + a. Je n'insisterai pas sur la notion de nombre réel, mais vous pouvez considérer qu'il s'agit de n'importe quel nombre (1; -5; 2,03; 1⁄3; la racine carrée de 2; le nombre π=3,1415...; etc.).
 |
| Niels Henrik Abel |
- euclidien, du mathématicien de la Grèce antique Euclide, ayant possiblement vécu vers 300 avant J.-C. On l'associe à la géométrie (la géométrie euclidienne) et à l'arithmétique. Vous avez tous pratiqué la division euclidienne à l'école primaire ! C'est la division posée « à la main », avec la barre qu'on appelle une potence. Par ailleurs, Euclide a axiomatisé la géométrie du plan, en définissant les 5 axiomes qui servent de base à la géométrie euclidienne.
 |
| Euclide |
|
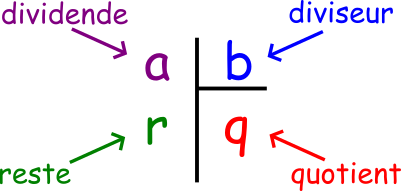 |
| La division euclidienne |
|
- hermitien, du mathématicien français Charles Hermite du XIXème siècle. Il est connu comme l'un des premiers à utiliser les matrices, entre autres contributions dans les domaines de l'algèbre et de l'analyse. L'adjectif matriciel se dit du calcul autour des matrices.
 |
| Charles Hermite |
|
 |
| Une matrice, tableau de nombres bidimensionnel |
|
- booléen, enne ou booléien, enne ou encore boolien, enne, de George Boole, logicien, mathématicien et philosophe britannique du XIXème siècle. Il est le créateur de la logique moderne, fondée sur une structure algébrique et sémantique, que l'on appelle algèbre de Boole en son honneur. On emploie aujourd'hui les termes de variable booléenne ou de booléen en informatique, pour désigner une variable à deux états (généralement notés vrai et faux).
 |
| George Boole |
- riemannien (anagramme : arminienne; construction : iranienne+M), du mathématicien allemand Georg Friedrich Bernhard Riemann du XIXème siècle. Il s'est consacré à l'analyse et à la géométrie différentielle; il a notamment mis au point une construction de l'intégrale (que Lebesgue, l'un des plus grands mathématiciens français du début du XXème siècle, généralisera plus tard). L'intégration est grosso modo le procédé de calcul de l'aire d'un domaine délimité par une courbe, et l'une des composantes fondamentales du calcul infinitésimal comme déjà mentionné ci-dessus.
 |
| Bernhard Riemann |
Géométrie
La géométrie est riche en vocabulaire pour désigner tous les différents types de figures.
En dimension 2 (dans le plan), les figures élémentaires sont les polygones, figures formées d'une ligne brisée fermée, c'est-à-dire d'une suite cyclique de segments consécutifs. La liste des polygones est la suivante :
- triangle (3 côtés), qui peut être isocèle (2 côtés de même longueur), équilatéral (tous les côtés de même longueur), rectangle (un angle droit), scalène (tous les côtés de longueurs inégales), obtusangle (un angle obtus)
- quadrilatère (4 côtés), dont les parallélogrammes, les trapèzes, les rectangles, les losanges, les carrés
- pentagone (5 côtés)
- hexagone (6 côtés)
- heptagone (7 côtés)
- octogone (8 côtés)
- ennéagone (9 côtés)
- décagone (10 côtés)
- hendécagone (11 côtés)
- dodécagone (12 côtés)
- téragone, polygone ayant un très grand nombre de côtés, sans en préciser le nombre.
Les adjectifs associés sont également valides (polygonal, pentagonal, hexagonal, ...), sauf téragonal.
 |
| Heptagone régulier inscrit dans un cercle |
Parmi les autres figures planes, on notera les coniques, qui sont de trois types :
- les paraboles;
- les hyperboles;
- les ellipses.
 |
| Une ellipse (en rouge), une parabole (en vert) et une hyperbole (en bleu) |
En dimension 3 (dans l'espace), l'"équivalent" des coniques (en un sens que je m'abstiendrais de préciser) sont les quadriques, qui se déclinent en une multitude de familles de surfaces différentes.
 |
| Les quadriques; de gauche à droite : hyperboloïdes à une et deux nappes, ellipsoïde (construction : éolipiles+D), paraboloïde hyperbolique (la selle de cheval !), cylindre, paraboloïde elliptique, cône |
Dans l'espace toujours, les solides sont des figures limitées par des surfaces indéformables, appelées faces. Si toutes les faces sont planes, on parle de polyèdre (anagramme : déployer), et on distingue ainsi, à l'instar des polygones :
- le tétraèdre (4 faces)
- le pentaèdre (5 faces)
- l'hexaèdre (6 faces), dont le rhomboèdre est un cas particulier (toutes les faces sont des losanges égaux; sous-top : mordorée)
- l'heptaèdre (7 faces)
- l'octaèdre (8 faces)
- le dodécaèdre (12 faces)
- l'icosaèdre (20 faces; sous-tops : croisade, décroisé, ...)
 |
| Rhomboèdre |
|
 |
| Icosaèdre |
|
On notera également :
- le cube, le prisme et la pyramide, qui sont des cas particuliers de polyèdres; on notera par ailleurs l'adjectif cuboïde, « qui a l'apparence d'un cube »;
- la sphère, premier exemple de solide qui n'a pas de surface plane;
- le tore (ou donut si vous préférez ! qu'on peut d'ailleurs également orthographier doughnut). L'adjectif toroïdal, ale, bien plus intéressant pour nous, qualifie ce qui est en forme de tore;
- l'adjectif et nom masculin conoïde, qui qualifie cette fois ce qui est en forme de cône.
 |
| Tore |
On termine le tour des figures de géométrie par un terme rigolo, patatoïde, utilisé pour évoquer une surface irrégulière ressemblant à une pomme de terre, ou simplement un objet sans propriété géométrique utile ou connue.
 |
| Un astéroïde de forme patatoïde |
On passera rapidement sur les transformations du plan : symétrie (centrale ou axiale), rotation, translation, homothétie, similitude, projection (orthogonale ou non). On munit souvent le plan d'un repère, généralement orthonormé. On n'oubliera pas les demi-droites (sous-top : miroitée), les demi-plans (construction : limande+P) et les demi-espaces (construction : pèse-acide+M).
 |
| Homothétie |
Le birapport de quatre points du plan, qui mérite d'être cité à part, est un nombre calculé à partir d'une formule dont on se passera, et surtout un outil permettant de déterminer si ces points sont alignés ou appartiennent à un même cercle. Il est essentiellement utilisé dans le contexte de la géométrie projective. Grossièrement, la géométrie projective du plan consiste à rajouter un point à l'infini... Si vous observez deux rails parallèles d'une ligne de voie ferrée, vous avez l'impression qu'ils se coupent à l'horizon, considéré comme l'infini !
D'autres adjectifs en vrac :
- colinéaire (sous-tops : acroléine, arénicole, câlinerie), pour parler de points alignés sur une même droite ou de vecteurs de même direction, un vecteur étant défini par un bipoint (c'est-à-dire un couple de points dont l'un est l'origine et l'autre l'extrémité);
- coplanaire, pour parler de points ou de droites situés dans un même plan;
- fractal, ale (construction de fractal : calfat+R; anagramme de fractale : calfater); une figure fractale, ou fractale, est en première approximation une courbe, une surface, un volume de forme irrégulière ou morcelée qui se crée en suivant des règles déterministes ou stochastiques impliquant une homothétie interne. Plus généralement, une fractale est un objet dont la structure est invariante par changement d'échelle. L'illustration de l'entête de l'article en est un exemple. En voici d'autres ci-dessous :
 |
| Construction étape par étape du flocon de Von Koch |
|
 |
| Construction étape par étape du tapis de Sierpinski |
|
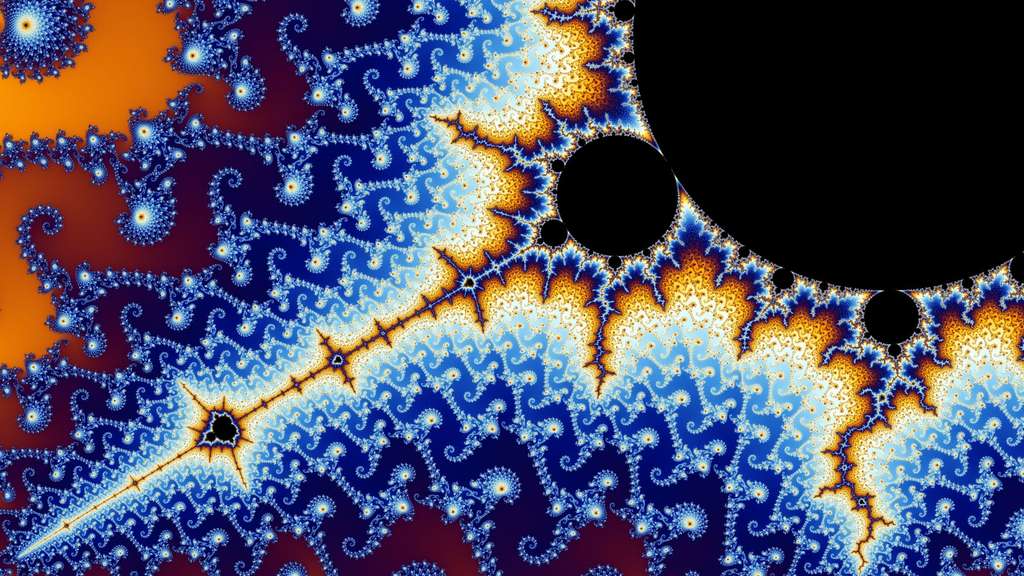 |
| L'ensemble de Mandelbrot |
Théorie des applications
En mathématiques, les applications sont des objets centraux; on les retrouve dans tous les domaines. Une application est une correspondance entre deux ensembles donnés, telle qu'à chaque élément du premier ensemble, on associe exactement un élément du second ensemble. Donnons un exemple concret qui servira de base pour le vocabulaire que nous allons décrire. J'ai un ensemble d'élèves et un ensemble de chaises dans ma salle de classe. Mon application consiste à installer chaque élève sur une chaise de mon choix.
- L'application est dite injective (de l'adjectif injectif, ive) si tous les élèves sont installés sur des chaises différentes. J'aimerais effectivement éviter d'installer deux élèves sur la même chaise !! On parle alors d'injection (sous-tops : ci-jointe, nicotine).
- L'application est dite surjective (de l'adjectif surjectif, ive) si toutes les chaises de la salle sont occupées... ce qui n'est possible que s'il y a autant ou moins de chaises que d'élèves ! On parle de surjection (sous-tops : courtines, jointures).
- L'application est dite bijective (de l'adjectif bijectif, ive) si elle est simultanément injective et surjective, c'est-à-dire si toutes les chaises de la salle sont occupées par un et un seul élève. Il faut pour cela qu'il y ait exactement autant de chaises que d'élèves. On parle de bijection (construction : ci-jointe+B), et dans ce cas, les deux ensembles (d'élèves et de chaises dans mon exemple) sont dits équipotents (sous-tops : pique-note, tonétique).

Analyse
L'analyse est la branche des mathématiques qui traite explicitement de la notion de limite, que ce soit la limite d'une suite ou la limite d'une fonction. Son point de départ est la formulation rigoureuse du calcul infinitésimal (rappelez-vous, Newton et Leibniz). Elle inclut également des notions comme la continuité, la dérivation et l'intégration. Dans un contexte plus général, on la retrouve par exemple en topologie (construction : otologie+P).
Dans le cadre restreint des nombres réels, les intervalles de nombres sont des objets centraux, et peuvent être ouverts (l'intervalle ouvert ]a,b[ est l'ensemble des nombres compris entre a et b exclus), fermés (l'intervalle [a,b] est l'ensemble des nombres compris entre a et b inclus), ou bien semi-ouverts (par exemple l'intervalle semi-ouvert ]a,b] est l'ensemble des nombres compris entre a exclus et b inclus; sous-tops : semi-ouvré, voiturées).
 |
| Les intervalles de nombres |
En ce qui nous concerne, l'analyse n'a pas beaucoup de vocabulaire à nous offrir. On passera sur les sempiternelles fonctions sinus, cosinus et tangente, d'usage en trigonométrie (parfois abrégée en trigo). D'autres fonctions, moins connues, se construisent à partir des trois précédentes :
- la sécante, définie comme l'inverse du cosinus (mot qu'on retrouve par ailleurs avec l'adjectif sécant, e);
- la cosécante (sous-tops : accostée, accotées, acescent, acétones), définie comme l'inverse du sinus (attention : pas de
cosécant !);
- la cotangente, définie comme l'inverse de la tangente.
Algèbre
L'algèbre est la branche des mathématiques qui permet d'exprimer les propriétés des opérations et le traitement des équations, et aboutit à l'étude des structures algébriques.
On lui associe la théorie des polynômes, et on parle de monôme (construction : nommé+O) et de trinôme pour citer quelques termes.
L'algèbre générale s'intéresse aux structures algébriques : les groupes (et leurs sous-groupes), les anneaux, les corps, les espaces vectoriels. Ces derniers font d'ailleurs l'objet d'une théorie plus spécifique, l'algèbre linéaire, dans laquelle on retrouve les matrices et le calcul matriciel, entre autres termes comme scalaire (non, ce n'est pas qu'un poisson, Arielle !), n-linéaire (construction : linéaire+N !), bilinéaire (construction : baleinier+I), que j'évoque sans précision. Pour comprendre les structures et les liens entre elles, on utilise des applications particulières qu'on appelle des morphismes (sous-tops : orphisme, pommiers); deux structures "équivalentes" sont dites isomorphes (sous-tops : orphisme, morphose).
Enfin, les nombres font bien sûr partie des études algébriques. De ce point de vue, je mentionnerais seulement les termes demi-entier (la moitié d'un nombre entier impair; construction : déterminé+I) et quaternion (sous-tops : nautonier/touranien, roquentin).
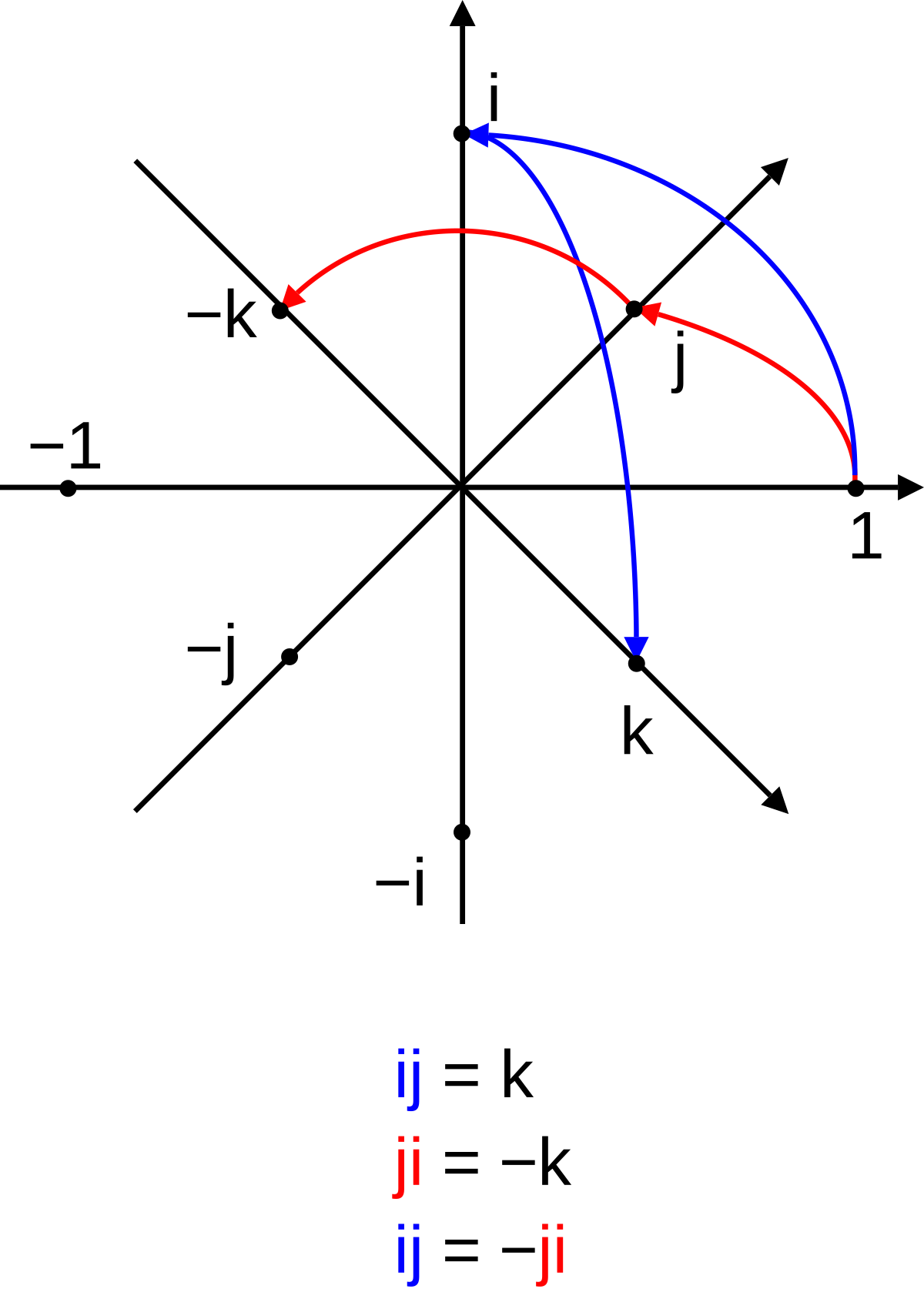 |
| Les quaternions |
Voilà qui conclut cet article mathématique. J'espère qu'il vous aura plu et vous aura montré une petite partie de l'immense étendue de cette science, qui a encore tant de choses à nous apprendre...
Bonne journée !

















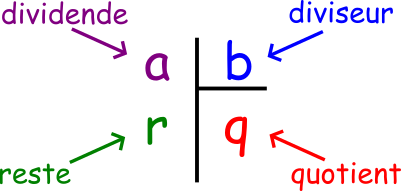



J'ai eu l'occasion, il y a 25 ans environ, d'assister à une conférence de Benoît Mandelbrot, père des fractales. Cet homme était passionné et passionnant !
RépondreSupprimerOn peut préciser qu'il existe un verbe PYRAMIDER…"disposer en pyramide "
RépondreSupprimer